LAB 3 - Jesse and Shingo CS40/ENGR26

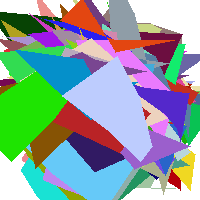
Required image: Shaded stardestroyer demonstrating filled polygons

LAB DESCRIPTION

This lab involved the the generation of a polygon and polyline class, the creation of filled primitives, testing the speed of these functions, and generating a picture using them. Most of the work was based on functions from the last lab such as the function to draw circles. In this case, code was modified and added to fill in the pixels inside the shape.

The polygon and polyline libraries are very similar. The polygon is simply a polyline in which the last vertex is the first creating a closed shape. The polygon can be filled using a scanline fill algorithm, but the polyline cannot. Here I will discuss the polygon library, but the description also applies to Polyline. The polygon library has functions to allocate memory and create template data structures. These are Polygon_create and Polygon_init. To set a polygon, a list of points can be passed in to the polygon data structure via Polygon_set. Polygon_drawFrame draws an outline of the polygon to the screen by taking subsequent points and using the line function, drawing lines between these points. Polygon_drawFill uses the scanline fill algorithm provided courtesy of Prof Maxwell. We are responsible for filling in key parts of the code.

The next part of the lab involved filling in circles and ellipses. The circle and ellipse code used to draw outlines draws one eigth of the shape and duplicates it around the circle 8 times so that it draws all the quadrants in simultaneously. To fill in these shapes, the drawing code was modified so that as pixels are filled in around the edge of the circle, it holds the y-value constant, and scans fills through the varying x-values. So at each step, we are drawing in 4 stripes into the circle. Same thing goes for filling the ellipses as well.

Testing the speed at which these filled primitives can be drawn to screen is the final part of the lab. To test circles, the same code used to test lines in the previous lab was utilized. Points now form radii and centers of circles rather than endpoints of lines. The code to test the speed of drawing polygons is considerably more complicated, but works on the same principles. We wanted to randomize the number of vertices in each polygon generated, but that would have resulted in a tricky allocation of memory (and we wanted to allocate memory before actually running the test, to not cut into the test time). Therefore we just draw hexagons of varying sizes.

hexagon

Required image demonstrating primitives

polygon

QUESTIONS

1. Is your polygon algorithm consistent with respect to screen coordinate issues, and does it produce rectangles that are the correct area? What changes to the algorithm did you have to make in order to make it consistent? You might want to make a simple image to demonstrate the mathematical consistency on your web page.



We defined a rectangle with 4 points, (1, 1), (9, 1), (9, 9), (1, 9). The area of the rectangle (in this case a square) should be (9 - 1) * (9 - 1) = 64. Our program indeed prints out a square with 64 pixels.


Image of rectangle from point (1,1) to (9,9) with area 64 - enlarged for the web (not to scale)




2. How many filled polygons of a reasonable (400 pixels < area < 1000 pixels) size and complexity (5-7 edges) can your algorithm draw in 1 second?



Our program can draw about 18,000 hexagons per second. They vary in area, their perimeter can be up to 250 pixels (see below).


Polygons generated using the speed test code




3. How many filled circles of a reasonable size (10 pixels < r < 20 pixels) can your algorithm draw in 1 second?



Our program can draw about 260,000 to 300,000 circles of area 390 pixels (on average) per second.



Circles generated using the speed test code




4. If you extended this assignment in any way, describe what you did and how you did it. Include pictures, or links to pictures that show what you did.

Recognize this?