LAB 10 - Jesse and Shingo CS40/ENGR26


HOME Lab1 Lab2 Lab3 Lab4 Lab5 Lab6 Lab7 Lab8 Lab9 Lab10 CODE
Jesse's Portfolio Shingo's Portfolio


LAB DESCRIPTION

For the final assignment, we have been given the liberty to choose our own topic. Note that the final assignment is optional and may be viewed as a set of extensions. This lab focuses on primitives, the backbone of an interesting 3D scene.



PRIMITIVES

  1. Bezier Spline

    2. Splines are smooth curves generated based on a given set of points. This extension uses deCastalau splines. 4 vertices in world coordinates outline the spline. Once a resolution is set, midpoints between the vertices are recursively used to draw new lines. Given a threshold of only a few pixels, the resulting picture is a smooth looking curve with endpoints at the first and last vertices specified. Our new spline library provides the added functionality of drawing dashed splines.


    Spline demonstration

  2. Spheres, Asteroids, and octahedrons

    3. Method #1 as shown below was the first attempt at creating a sphere. It subdivides the sphere into rectangular faces using angles theta and phi. (see code: sphere_test.c). The program was eventually discarded in favor of a method resulting in triangular faces (method #2 below). The second version thus uses the method of recursively subdividing the faces of an octagon. Asteroids can easily be made by adding a random offset to the radius when points are pushed to the edge of the sphere after subdivision.


    Sphere method #1 using rectangular faces
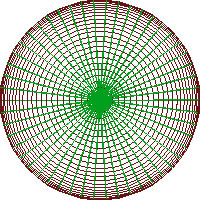    Sphere method #2 using triangular faces

    Sphere with 6 levels of recursion