Abstract
In this lab the system parameters for a DC motor system were determined. The motor was attached to a tachometer, flywheel, and a load motor. Data was acquired for the unloaded spin up of the motor, as well as the response of the system upon the application of a load. The data values compared favorably to those determined in previous years.
Derivations
To measure the constants km and R, we can use equations 3 and 5,
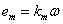 (1) (1)
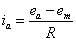 (2) (2)
Divide by 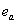 , ,
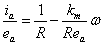
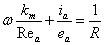
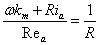
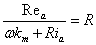
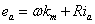
Finally,
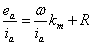
Since we have measured values for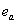 , ,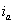 , and , and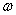 , we can plot , we can plot 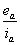 versus versus 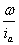 to determine the slope and intercept, which reveals the constant values of to determine the slope and intercept, which reveals the constant values of 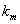 and R. and R.
To derive B, tf, and kw we use the equation
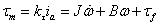
For steady state 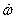 = 0, so we have = 0, so we have
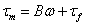
If we plot the graph of 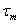 versus versus 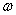 , and plot a best fit line we get , and plot a best fit line we get
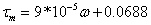
This corresponds to a B value of 9*10-5. and a 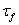 value of 0.0688. value of 0.0688.
Once we know 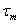 , we can find , we can find 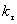 using using
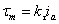
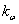 is the slope of the is the slope of the 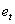 vs vs 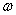 graph and is 0.0128. graph and is 0.0128.
Results
The system parameters for the DC motor are summarized in the graphs and tables below. Setup 1 was used in determining the parameters.
Figure 1. Graph used to determine kw.
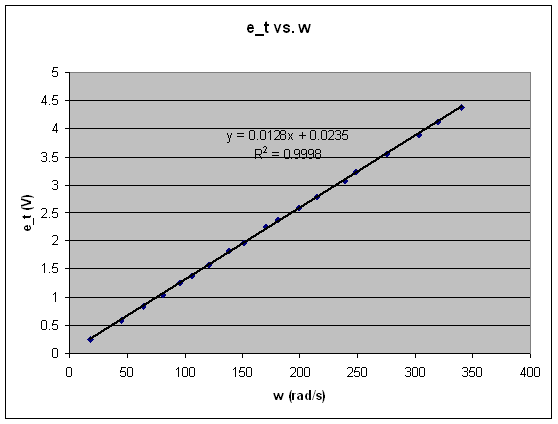
Figure 2. Graph used to determine constants km and R.
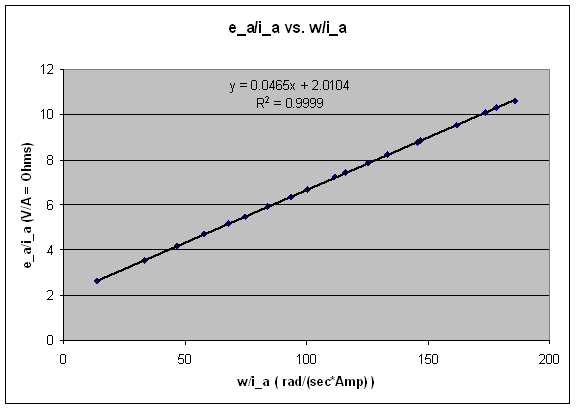
Figure 3. Graph used to determine B and Tf.
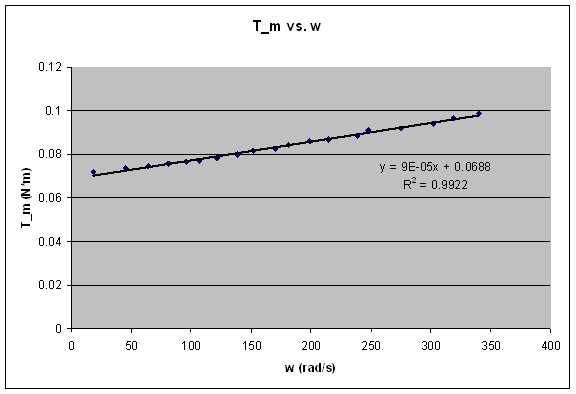
Table 1. System Parameters
kw |
B |
R |
km |
Tf |
kT |
0.0128 |
9.00E-05 |
2.0104 |
0.0465 |
0.0688 |
0.054 |
Viscous Friction vs. Coulombic Friction
We estimate the speed at which the viscous friction is greater than the coulomb friction, that is, when 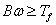 . The speed can be calculated by dividing Tf by B: . The speed can be calculated by dividing Tf by B:
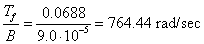
The approximate tachometer voltage corresponding to this speed can be determined by using the best fit equation for the relationship between et and w. The best fit equation is: 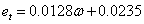 . Plugging in w calculated above, we get an expected tachometer voltage: . Plugging in w calculated above, we get an expected tachometer voltage:
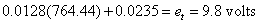
This voltage is nearly double any tachometer voltage determined in the lab. As such, we can assume that the Coulomb friction in the motor system dominates.
Calculating J from the Motor Spinup Data
Applying a step input of 18 volts to the motor, and acquiring data samples at 60 Hz, we obtained a curve for the tachometer voltage vs. time. Given the form of the first order response of the system to an input, we fit the data with an appropriate exponential to determine the time constant.
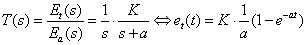
where
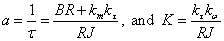
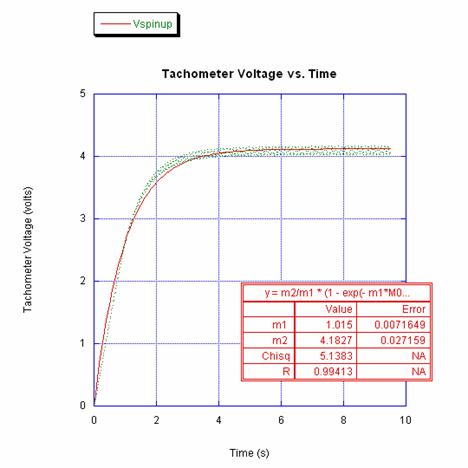
Using the above equations and the best fit constants for the motor spin up obtained above, we calculate
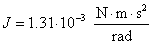
System Transfer Function
The theoretical response of the system given the calculated parameters is shown below:
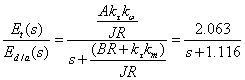
Applying a step input of 2.5 volts, the result obtained in MATLAB is shown below, graphed next to the experimentally obtained data.
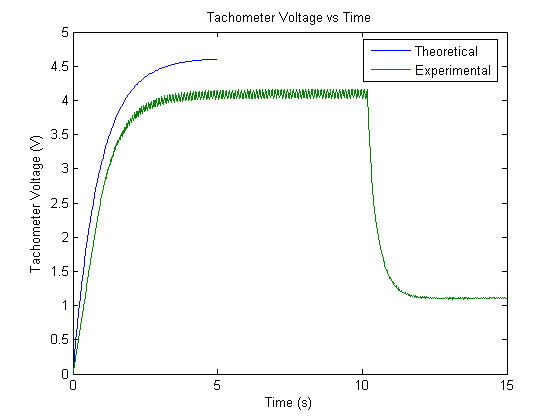
The difference in steady state value can be accounted for by the nonlinear coulomb friction that the current transfer function neglects.
Applying the Load Motor
Throwing the switch to short out the leads of the load motor causes the rotation to slow down. The tachometer voltage is shown below as a function of time.
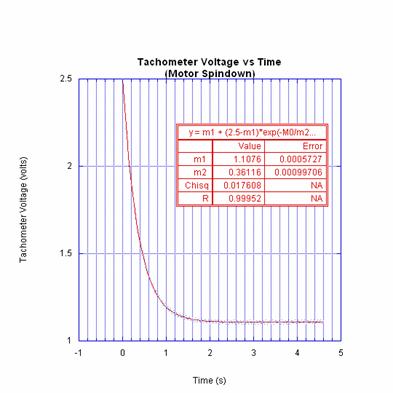
For the motor spin down, we see that the final voltage is 1.1076 V, which is a 75.3 % drop from the original steady state voltage of 4.12 V.
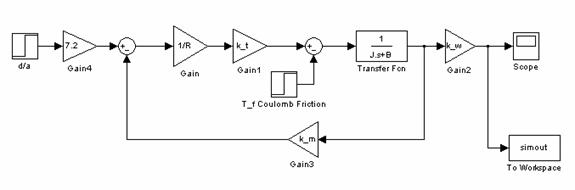
Simulink Model Accounting for Coulomb Friction
The Simulink model including Coulomb friction is shown below.
Simulating the model and plotting it against the experimental data results in the graph below.
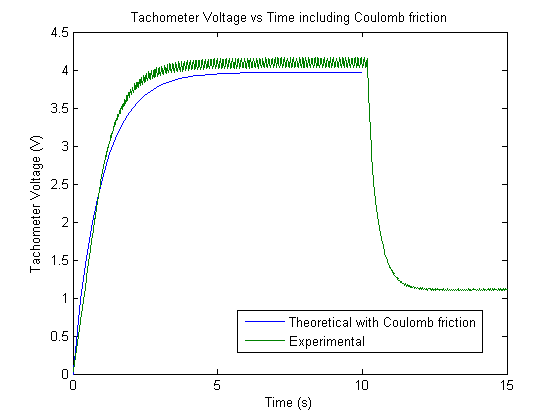
Accounting for the Coulomb friction makes the theoretical data agree better with the experimental data.
Matlab Motor Control and Data Acquisition Control Code
clc;
SampleFreq=60;
NumPts=SampleFreq*15;
PreSample=0;
InChan=0;
OutChan=0;
DT=1/SampleFreq;
Ain = analoginput('nidaq');
Ain.SampleRate=SampleFreq;
Ain.SamplesPerTrigger=NumPts;
Ain.InputType='SingleEnded';
Ain.BufferingConfig=[1 2000];
Ain.TransferMode='Interrupts';
addchannel(Ain,InChan);
Aout = analogoutput('nidaq');
addchannel(Aout,OutChan);
OutData=zeros(NumPts,1);
t=((1:NumPts)-PreSample)*DT;
LastIndex=0;
start(Ain);
putsample(Aout, 2.5);
while (Ain.SamplesAcquired<NumPts),
j=Ain.SamplesAcquired;
while(LastIndex==j),
j=Ain.SamplesAcquired;
end
if ((j-LastIndex)~=1),
disp(sprintf('Warning, datum skipped: %d, %d',LastIndex,j));
end
InData=peekdata(Ain,j);
if (t(j)<0),
OutData(j)=0;
else
OutData(j) = InData(j);
end
LastIndex=j;
end
putsample(Aout,0);
delete(Ain)
clear Ain
delete(Aout)
clear Aout
plot(t,InData,t,OutData)
xlabel('Time');
ylabel('Voltage');
title('Tachometer Voltage vs time');
save 'MyData' t InData OutData |