This lab was an introduction to the data acquisition system; we learned how to use MatLab® to code and run simple programs and to work with a signal generator and an oscilloscope. The lab instructions can be found here.
TASKS
2a) graphs showing the input and output results when the signal is at 5, 10, 20, 40, 50, 60 and 80 Hz. Sampling rate = 100 Hz.
We defined the output function to be -1/2 * Vin.
For graphs that have input signals with frequencies below 50 Hz looked perfectly fine in the acquired signal since the sampling frequency was 100Hz. For input signals that have frequencies of 50Hz and higher, the acquired signals looked as we expected them to be, but they didn't represent the actual signals because the Nyquist criterion was not met. That is, the sampling frequency was less than twice the maximum frequency of the signal, which can result in aliasing in the data acquisition. Graphs 5 through 7 show this aliasing effect occurring.
For an input signal with a frequency of 200 Hz, the acquired signal almost resembled a straight line (it should resemble a straight line), because the signal was always sampled at the same amplitude. In graph 26, the acquired signal looks like a straight line and we would expect it to be a straight line but it is slightly curved. This is because the sampling frequency does not match the input signal exactly.
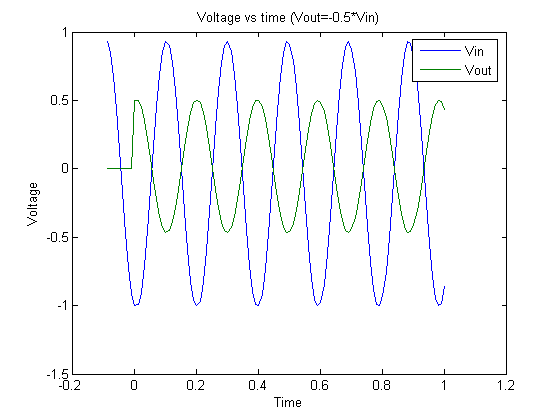
Graph 1. 5Hz signal and output.
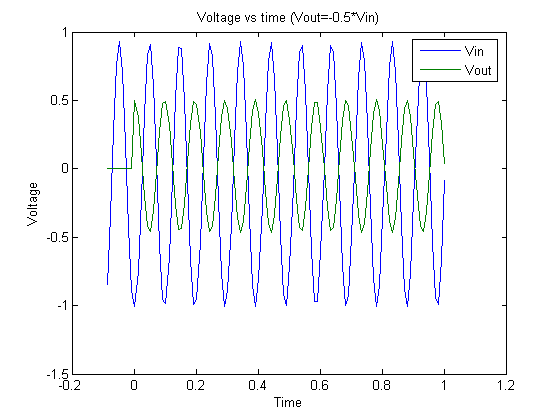Graph 2.10 Hz signal and output.
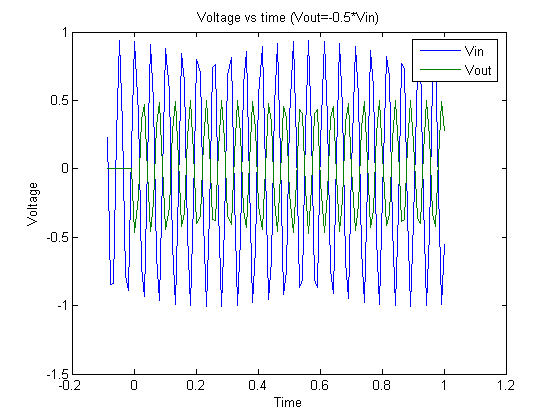
Graph 3. 20Hz signal and output.
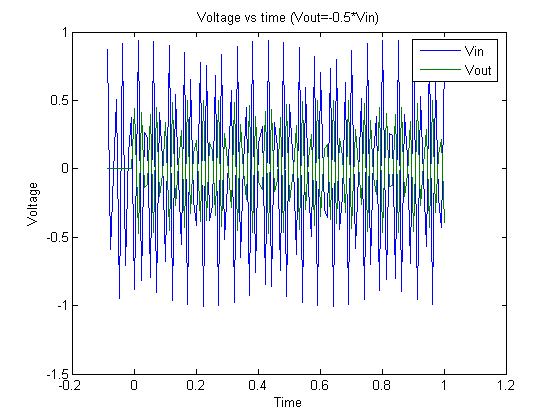Graph 4. 40 Hz signal and output.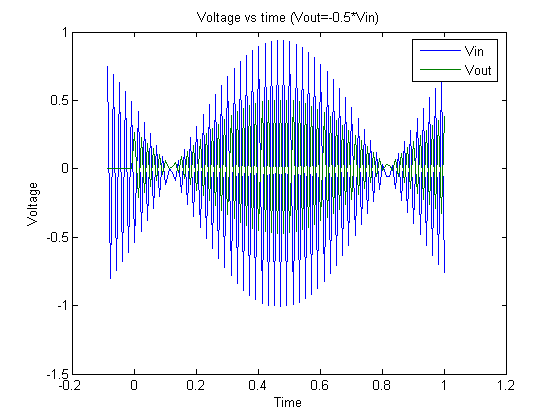 
Graph 5. 50 Hz signal and output.
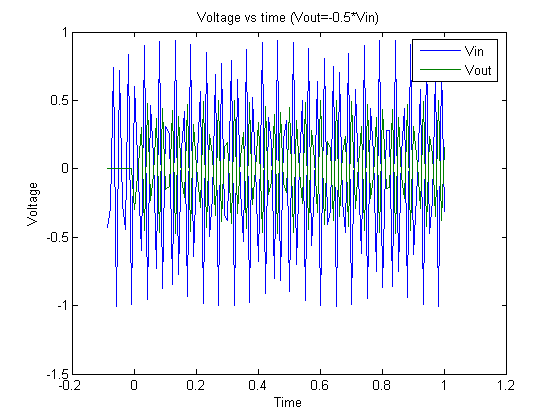Graph 6. 60 Hz signal and output.
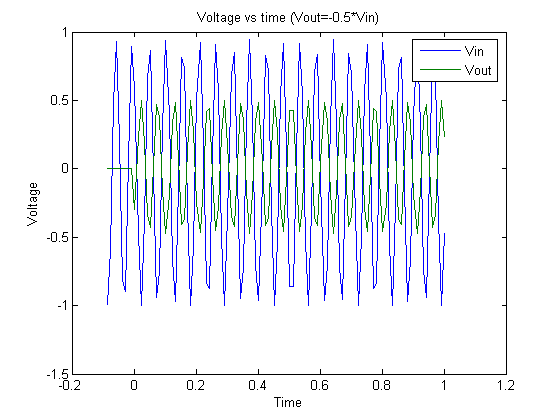Graph 7. 80 Hz signal and output.
2b) Modifying the program so that the output is equal to the average of the previous 5 inputs. Graphs show the input and output results when the signal is at 5, 10, 20, 40, 50, 60 and 80 Hz. Sampling rate = 100 Hz.
For this task we averaged the five previous inputs. Here is the code we added to accomplish the task.
Control algorithm for averaging the last five inputs.
if (t(j)<0), %If during PreSample, output 0.
OutData(j)=0;
else %Else, do control algorithm
OutData(j)= ( InData(j) + InData(j-1) + InData(j-2) + InData(j-3) + InData(j-4) ) / 5;
%this takes the average of the previous five inputs
end
putsample(Aout,OutData(j));
On the graphs, the output signal is 0 for ten samples (0.1 second) this is because we set the pre-sampling period to 10 samples. In pre-sampling the program still acquires data, but does not output a signal.
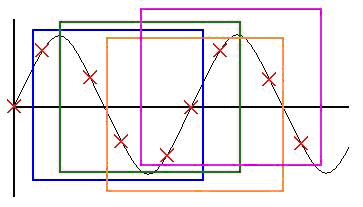
Figure 1. 20 Hz signal sampled at 100 Hz.
The acquired graphs match our expectations. For the 20 Hz signal we expected to get a straight line because as seen in figure 1 every new sample was supposed to match the signal being omitted from the inputs that we averaged. In figure 1 every colored box represents a group of 5 samples, and as you (prof.Cheever) may readily observe, the average of the samples in every box is the same.
For the graphs with frequencies above 50 Hz, we observed aliasing because the sampling frequency was no longer at least twice the input frequency.
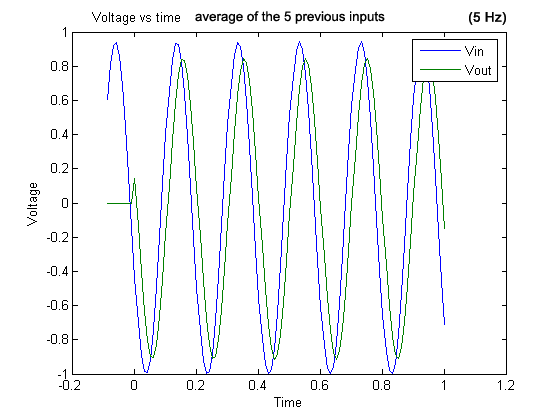
Graph 8 . 5 Hz signal and output (average of the five previous inputs).
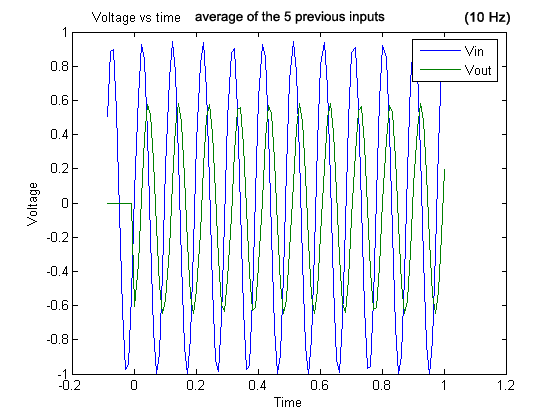
Graph 9 . 10 Hz signal and output (average of the five previous inputs).
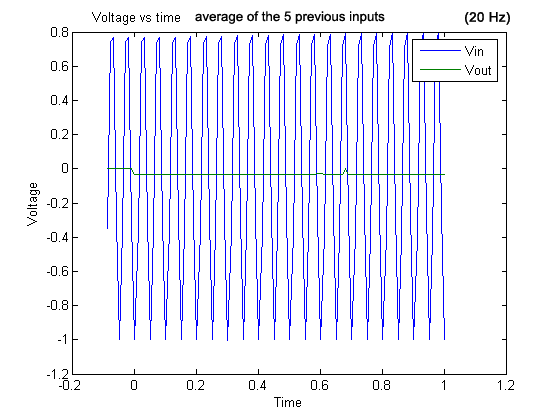
Graph 10 . 20 Hz signal and output (average of the five previous inputs).
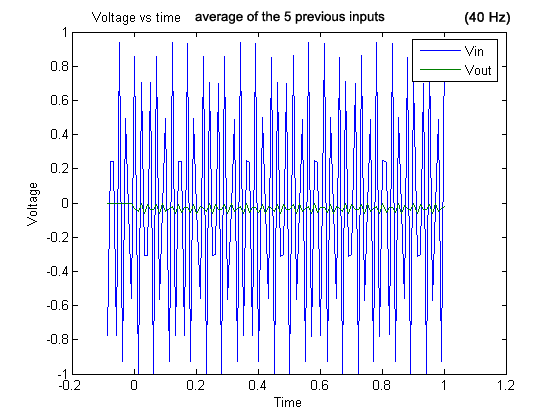
Graph 11 . 40 Hz signal and output (average of the five previous inputs).
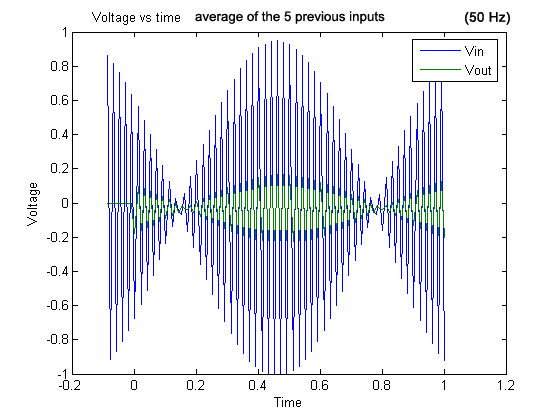
Graph 12 . 50 Hz signal and output (average of the five previous inputs).
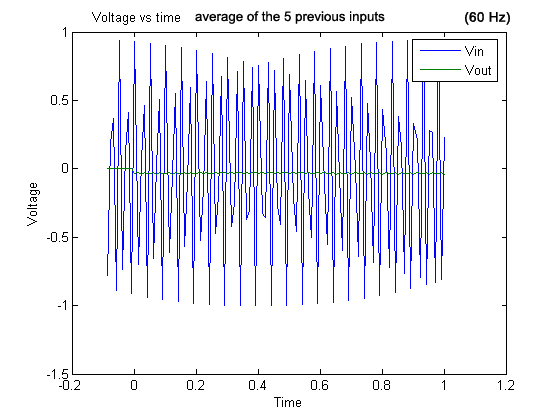
Graph 13 . 60 Hz signal and output (average of the five previous inputs).
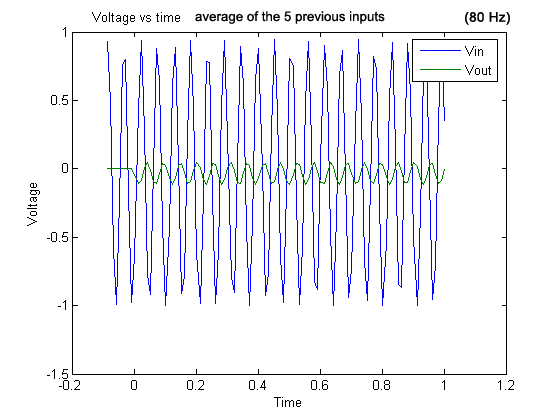
Graph 14 . 80 Hz signal and output (average of the five previous inputs).
2c) Modifying the program so that the output is equal to the difference of the previous 2 inputs. Graphs show the input and output results when the signal is at 5, 10, 20, 40, 50, 60 and 80 Hz. Sampling rate = 100 Hz.
For this task we took the difference of the two previous inputs. Here is the code we added to accomplish the task.
if (t(j)<0), %If during PreSample, output 0.
OutData(j)=0;
else %Else, do control algorithm
OutData(j)= InData(j) - InData(j-1);
%difference of the previous inputs
end
putsample(Aout, OutData(j));
As usual, the graphs reflect our expectations. With the signals that
do not meet the Nyquist criterion you can see dramatic aliasing
effects.
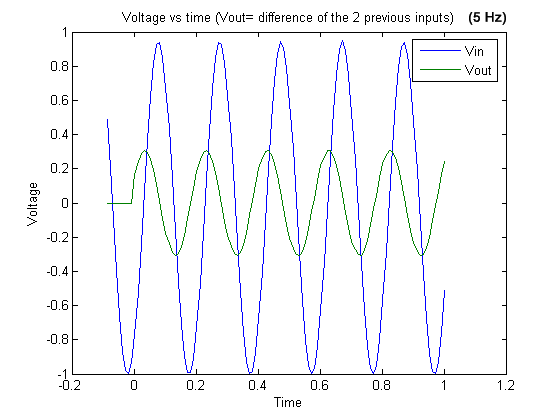
Graph 15. 5 Hz signal and output (difference of the two previous inputs).
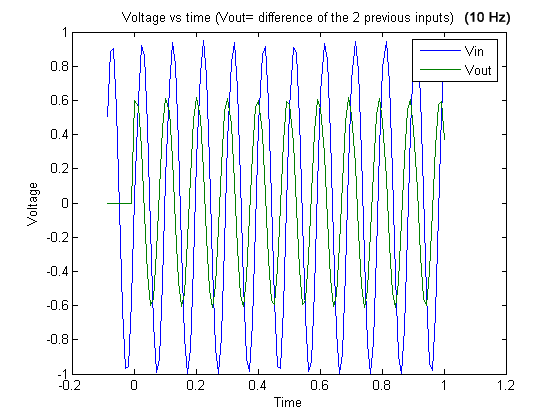Graph 16. 10 Hz signal and output (difference of the two previous inputs).
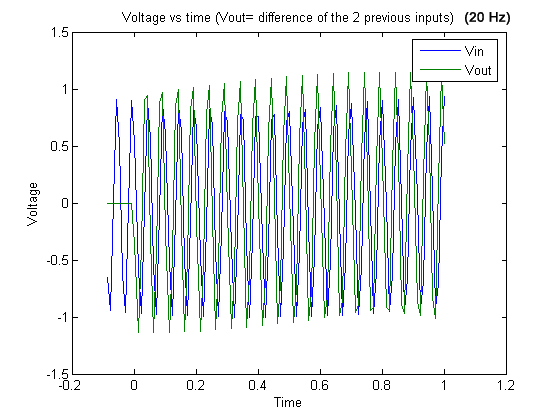Graph 17. 20 Hz signal and output (difference of the two previous inputs).
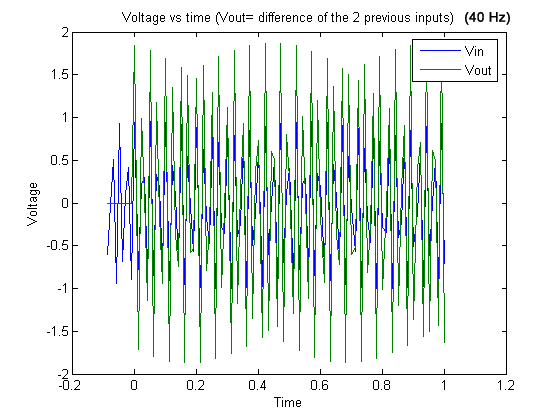Graph 18. 40 Hz signal and output (difference of the two previous inputs).
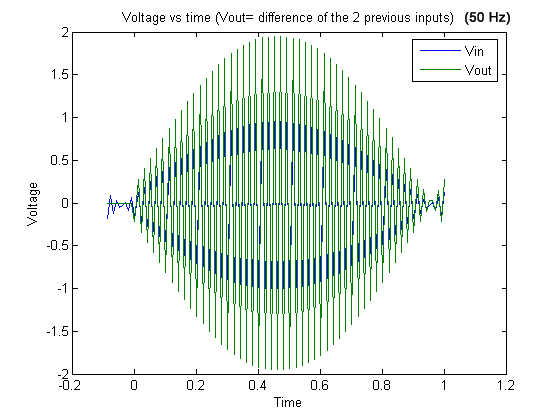Graph 19. 50 Hz signal and output (difference of the two previous inputs).
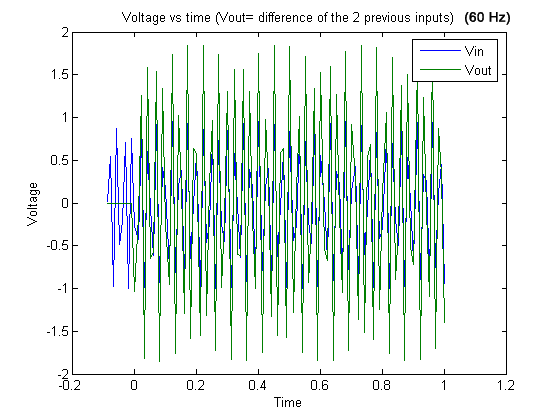Graph 20 . 60 Hz signal and output (difference of the two previous inputs).
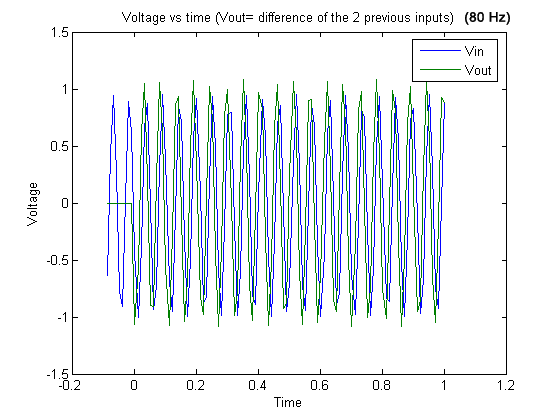Graph 21 . 80 Hz signal and output (difference of the two previous inputs).
EXTENSIONS
For 100 Hz signals, since the input signal and the sampling frequency are not exactly the same, we did not get a straight line for both the input signal and the output signal. (Graph 22)
As an extension we wanted to show how we could make the output and
input both equal zero using 200 Hz input signals, but even then it was
impossible to obtain a signal at exactly 200 Hz. However, you can see
that the output signal is almost flat near zero.
Also as an extension, we tried to plot the difference of the two
previous inputs of 98Hz (Graph 23) and 102 Hz signals (Graph 24). The
aliasing effect is obvious.
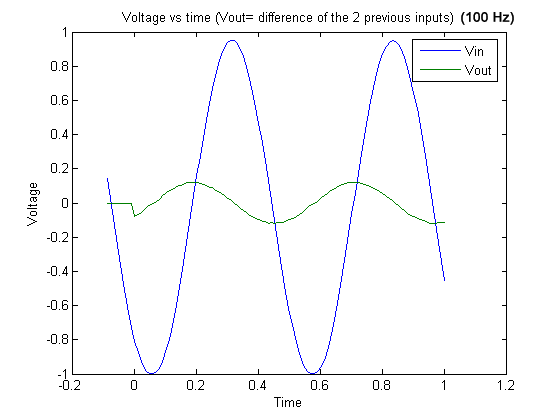Graph 22 . 100 Hz signal and output (difference of the two previous inputs).
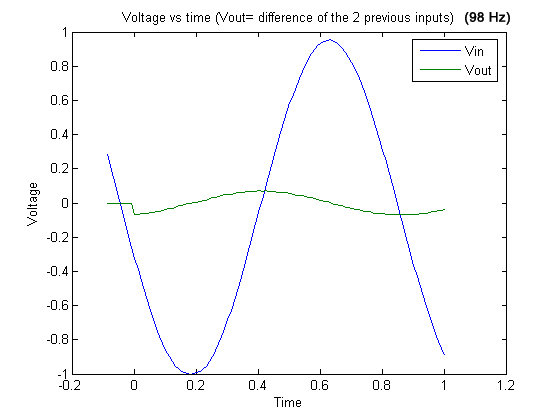Graph 23 . 98 Hz signal and output (difference of the two previous inputs).
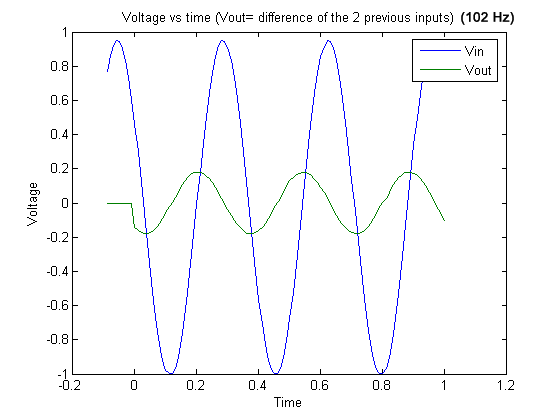Graph 24 . 102 Hz signal and output (difference of the two previous inputs).
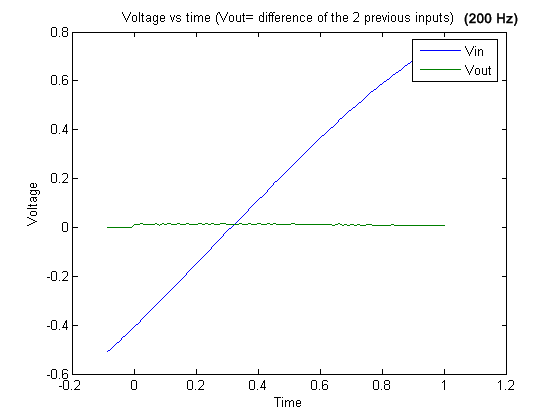Graph 25 . 200 Hz signal and output (difference of the two previous inputs).
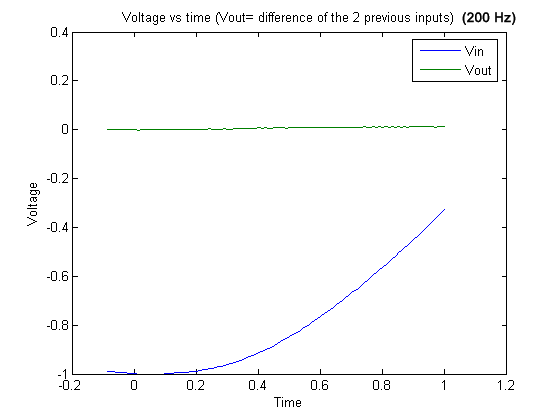Graph 26 . 200 Hz signal and output (difference of the two previous inputs).
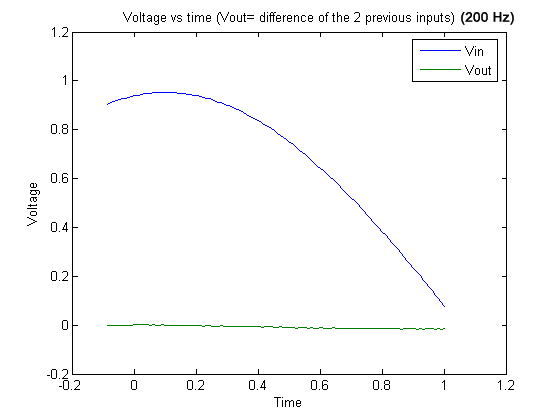Graph 27 . 200 Hz signal and output (difference of the two previous inputs).
|