The vertices in figure 1 represent the possible couples. Vertex 1 represents (m, w), vertex 2 represents (m, w’) and so on.
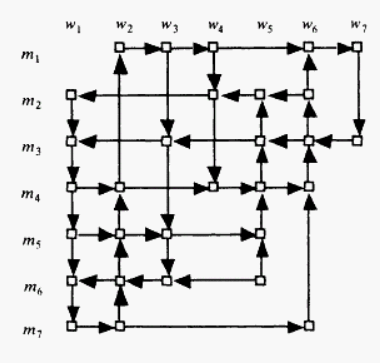
We can add arcs to this graph to represent the preferences of the stable marriage participants. A vertical arc (in figure 1 an arc going in either direction between 1 and 3 or 2 and 4, in either direction) represents the preference of the woman at the head of the column. If, for example, woman w prefers man m to man m’, we will draw the arc arc (3, 1) in the picture in figure 1. Similarly, horizontal arcs represent the preferences of the men. In a stable marriage instance with more than two participants of each gender, there will be an arc between every pair of ranked men in any woman’s column, and similarly for every man’s row. The majority of these arcs are superfluous, however, since preference is transitive. So we can delete any arc implied by transitivity, and determine the preference order by examining the path from the least to most preferred in each column or row. A vertex may have a degree as high as four. A vertex with higher indegree than outdegree represents a couple that is popular with both genders, while one with higher outdegree than indegree represents a couple that is less popular. Figure 2, from Balinski and Ratier in 1998, shows the directed graph for a stable marriage problem instance with 7 men and 7 women. I’ve added a possible preference list for clarity. Note that not every possible couple has a vertex in the graph. The vertex can be omitted if either the man in that row or the woman in that column did not rate the other. No pair in which one participant finds the other so undesirable that he or she would rather be single could possibly be part of a stable marriage, so it does us no good to consider it.
Preferences: