Directed Graph Algorithm
The directed graph representations of the stable marriage problem shown on
the previous page facilitate another algorithm and proof that produce the same
stable marriages as the Gale-Shapley algorithm. Like the Gale-Shapley algorithm,
directed graph algorithm always terminates, proving the existence of a stable
marriage for all instances of the problem.
Consider vertex v in a graph G of an instance of the stable marriage problem that has an arc going from it to another vertex in G. We’ll say that v has a successor.
Lemma 1: A matching M is stable iff every vertex not in M has a successor
in M.
Proof:
<-Let M be stable. Let v be a vertex in G but not in M representing the couple (m, w). Let m be paired with w' and w with m' in M. Assume towards contradiction that v has no successor in M. Then there is no arc from v to the vertex representing (m, w'), so m prefers w to w'. Furthermore, there is no arc from v to the vertex representing (m', w), so w prefers m to m'. This is a contradiction, so v has a successor in M.
->Now let every vertex in G be in M or have a successor in M. Let (m, w) be a pair represented by v who are not matched in M. Since m and w are not matched in M, v has a successor in M. If the successor is in the same column, m prefers his partner in M to w. If the successor is in the same row, w prefers her partner in M to m. Since there must be either a vertical or horizontal successor, m and w would not have an affair. So M is stable.
Consider a vertex of the following configuration:

These vertices are woman-best because each has a vertical arc entering but
not leaving it. So they must be the woman represented in that column’s
first choice. Man-best vertices are defined analogously.
A vertex in dominated in a graph G if it has a man-best successor in the same
column or a woman-best successor in the same row.
Lemma 2: Let G be a stable-marriage directed graph containing a vertex v. Let v be dominates by some vertex u. Then the set of possible stable marriages in G-{v} is equivalent to the set for G.
Proof: Let M be a stable marriage in G, let the vertex v
represent the couple (m, w) and let u represent (m, w'). Then v cannot be in
M because m is w'’s first choice and m prefers w' to w. Furthermore, by
lemma 1, every vertex in G is either in M or has a successor in M. Since v cannot
be in M, every vertex for which v is a successor must be in M or have another
successor in M. Since the deletion of v does not change any of these arcs, M
is stable in G-{v}, also by lemma 1.
Now, let M' be a stable marriage in G-{v}. Then by lemma 1, every vertex in
G-{v} is in M' or has a successor in M'. So every vertex in G-{v} is in M' or
has a successor in M'. But the vertex v has a woman-best successor, u, in the
same row. But either u is in M' or u has a successor in M', since u is in G-{v}.
We know that the successor of u must be in the same row as u since u is woman-best.
But then u’s successor is also a successor of v, since v is in the same
row as u. So v has a successor in M'. So, by lemma 1, M' is stable in G.
Note that an analogous lemma holds for a vertex which has a man-best vertex
as a successor in the same column.
Lemma 3: Let G be a graph with no dominated vertices. Then the woman-best (or man-best) vertices of G form a stable marriage.
Proof: Assume towards contradiction that the woman-best vertices
do not form a stable marriage. Then there must be some vertex woman-best vertex
v, representing the pair (m, w) that is not stable. Since this vertex is woman-best,
there is no arc from v to a vertex representing w and another man. So there
must be an arc from v to some other vertex in the same row, since m must prefer
some woman w' to w who prefers him to her assigned partner, m'. So there is
a vertical arc from the vertex representing (m', w') to v. But then we have
reached a contradiction, since (m', w') is in the original matching, so it is
woman-best and has no vertical arcs leaving it.
From this point, it is easy to construct an algorithm to produce a stable marriage from a directed graph. We must simply delete all dominated vertices and then find the woman or man-best vertices in the resulting graph. Consider the following example of the deletion process:
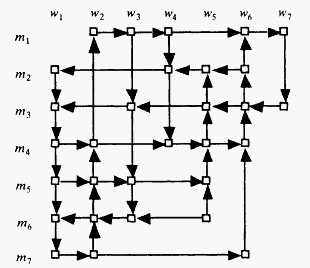
[BM1]
Graph before deletions
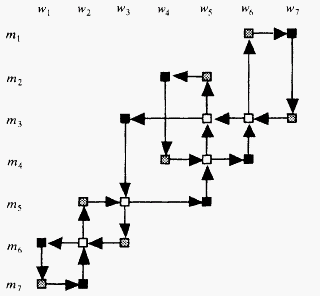
[BM1]
Graph after deletions
Note that in the graph after deletions, the black vertices are man-best and
the gray vertices are woman-best. Each set forms a stable marriage.