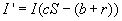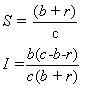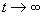Basic Concepts
Introduction
It is often desirable to be able to predict the spread and path of
diseases through a given population. Such knowledge can then be used to
help public health officials decide on appropriate response procedures.
Other information about the disease may be useful as well, such as the
total length in time of the epidemic, the rate of recurrence, the
equilibrium state of infectivity, or the effect of the initial infectant
on further propagation. In such situations, mathematical modeling can be a
useful tool.
Deterministic vs Stochastic
There are two basically different types of models for epidemiology,
deterministic models and stochastic models. Deterministic models assume all
contact rates between each infectious and susceptible person are equal, and
that a new infection will result from each of these contacts at some given
rate. Stochastic models, on the other hand, make use of probabilistic
factors to determine the rate of infection. Which of these types of models
is best suited to a given situation depends largely on the size of the
population, as well as its desired degree of precision.
Deterministic
As one might expect from their relative straightforwardness,
deterministic models have the longer history of the two groups. They have
been in use from the 19th century onwards. An important advance in the
development of deterministic models came from Kermack and McKendrick’s
study of mouse epidemics. Their work in this field led to the establishment
of the Threshold Theorem, which states that “the introduction of infectious
cases into a community of susceptibles would not give rise to an epidemic
outbreak if the density of the susceptibles were below a certain critical
value.” (Ref 1) These are the types of models
that we will be focusing on.
For a large population, or when little precision is necessary, the
difference between the performance of a deterministic and a stochastic
model is insignificant. A deterministic model is therefore probably
preferable, due to its relative simplicity.
Stochastic
Stochastic models are the younger of the groups. McKendrick came up
with the first epidemiological stochastic model in 1926. They did not come
into use for another 20 years, however. In terms of application, stochastic
models become preferable at small populations, particularly as small as a
household, when enough precision is required to outweigh the added complexity
of the model.
A Model of childhood disease (chicken pox)
One of the simplest disease models that one can study to some depth is a
childhood disease like chicken pox. With a disease like chicken pox, all
recovered people become immune to the disease (with insignificant exceptions).
Also, the latency between being infected and showing symptoms is very small.
One can therefore assume that all people who recover are effectively removed
from the population, and that there is no exposed group (which is present in
most other disease models), who have been infected but have not yet become
infectious.
The other assumptions made for this model are that all susceptibles are
equally susceptible, all infectious people are equally infectious, and that
the population remains fixed (by balancing birth with death and emigration).
The actual model
The total population (n) is divided into three groups: susceptibles (S),
infectious (I), and recovered (R), each of which is a fraction of the total
population, such that at all times,
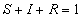
Let rb be the average birth rate (and thefore the average
death/emigration rate), and bc the contact rate, which is the average fraction
of susceptibles to contract the disease from a single infective.
Then the rate of change of the number of susceptibles in the population
is given by
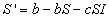
that is the birth rate minus the number of susceptibles who leave the
population by death or emigration minus the number of susceptibles who become
infected.
Now, let cr be the recovery rate, the average number of infected people
to recover per unit time, or 1/c is the mean infectious period. The rate of
change of the number of infected people is then
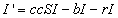
the number of people who become infected minus the number who leave due
to death or emigration minus the number who recover.
Finally, the recovered populations rate of change is given by
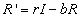
the number of people who recover from infection minus the number who leave
the population due to death or emigration.
Since the equations for S and I are independent of R, the system of
equations can be simplified to not include R explicitly, since it can be expressed
in terms of S and I:
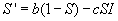 and
and
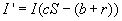
Furthermore, the solutions for these two equations must be nonlinear, due to the
presence of the product SI. Finding exact solutions to nonlinear differential
equations is particularly difficult. This can be accomplished in two different ways.
The first is to use a numerical method, such as Runge-Kutta to approximate the
solution. Otherwise, we can linearize the system of equations and find the solutions
around the critical points to find an approximate solution. One way to do this is by
the nullcline approach.
We set S’ and I’ to zero, and solve the resulting system, obtaining
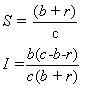
This is then the critical point where the equilibrium is defined. When shown in the
SI-plane, this point gives the solution to the linear portion of the system around
which the nonlinear portion oscillates. Since the system is stable, it should converge
to this point as 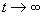
This value of S is also the threshold defined by the Threshold Theorem. In order
for I to be positive (nonzero) at equilibrium, this value must be less than one.
If I is not positive, then there are no infected people at equilibrium and there is
no epidemic. Then, for a small enough ratio of r to c, decreasing the contact rate
can have a significant effect, and the severity of the epidemic can be reduced or
even eliminated by the implementation of public health measures such as isolation of
infectives or vaccination of susceptibles.
This solution suggests that there should be recurring outbreaks of diminishing
severity after the initial outbreak. This pattern is not quite what is observed,
though. In fact, it is found that the severity of epidemics can depend on a number
of other factors, including seasonal changes. The model can then be refined by
making b a function of time rather than a constant, to portray a higher susceptibility
during winter months than during the summer. By adding this seasonality function,
apparently random fluctuations that look chaotic are observed.
(Ref 2) The system,
though perhaps aperiodic, is stable though, so not actually chaotic.
Back to main.
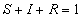
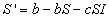
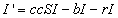
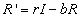
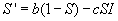 and
and