In this lab I worked with Sven on implementing
a version of multiple
dispatch in C++. Our initial approach was to have a highly
automated method of determining inheritance relationships, but that
turned out to be exceedingly difficult, and so our final solution is
heavily scaled back.
Representation
Internally we represent each vertex in our class
hierarchy as a templated node. To ease memory management, we maintain a
vector of pointers to these nodes, which is where all new vertices are
added and where the objects are deleted from at the end of the dispatch
object's lifetime. Whenever a vertex needs to refer to another vertex
(for inheritance relationships), it will store the index of its
relative in the array.
Thus each vertex in our graph stores an int vector representing its
children and another representing its parents. The graph object, which
manages these vertices, also stores a vector holding which vertices are
leaves. It can be told to regenerate this list, which the dispatch
object automatically does for you, at the appropriate time.
The dispatch object stores N graphs (one for each object of the
dispatchable type). Currently only the 2 dimensional case is
implemented; however, expanding to a greater number should be
relatively simple. Internally, some treacherous template games are
played so that the function pointers can reflect their true type, while
storing them internally in a single vector (which does not allow
disparate types).
Interface
A user will interface to the dispatch class by
constructing a templated dispatch object. The arguments to the template
are the base type for each of the object types and the return type.
int c1_id,c2_id;
disp< c1, c2, returnType > dispatcher( &c1_id, &c2_id,
defaultFunction );
The arguments to the constructor are two pointers to ints (used to store the id of the class object) and a pointer to the default function.
The user then adds a vertex to the disp object, for each type she wishes to place in the object hierarchy. These functions are templated and return the object's code.
int c1_child_id =
dispatcher.vertex_add_1< c1_child >();
Unfortunately, g++ has a bug in its implementation of templated member functions, so this has to be called
int c1_child_id =
dispatcher.template vertex_add_1< c1_child >();
Sadder still, MSVC has a bug in its templated member functions such that it does not even support them. While one could work around this problem by templating a normal function and then passing it a templated struct, this requires around 5 template arguments for each templated function.
Next the user must tell the dispatch object the proper hierarchy for each inheritance tree. We would like to automate this step; however, we have not yet stumbled upon the proper algorithm for determining these at run-time. The user creates this hierarchy by calling the dispatch object edge_add function for each of the inheritance links that need to be made, using the ids that have been gathered in previous steps. The syntax is edge_add( parent_id, child_id).
dispatcher.edge_add_1( c1_id,
c1_child_id);
It is worth note that there exist vertex_add_2 and edge_add_2 functions with the same syntax that are used to build up the other class's inheritance tree. If we can manage to automate this step (the edge adding), then the entirety of graph generation can be done silently during the next stage.
At this stage, the user supplies the functions that should be called for the different object types. This function is also templated, so the above notes about member templating still apply. The user should pass the function the ids representing the classes and the appropriate function pointer.
dispatcher.add< c1_type,
c2_type >( c1_type_id, c2_type_id, specificFunction );
As mentioned, if we can automate the graph generation only this final step will be necessary; however, every type of class for which this is done then must be default constructible. In the mean time, this manual approach will have to suffice. Once the dispatch object is constructed fully enough to support all of the specific functions that the user wishes to provide, the user can simply call the dispatch function on pointers to types derived from the base class even if those types do not directly appear in constructed graph.
dispatcher.dispatch(
c1_relative, c2_relative );
This function will call the appropriate specific function and return its result, which function is chosen is carefully defined in the next section.
Multiple Dispatch Ambiguity Resolution
Clearly, given arbitrary object hierarchies ambiguous
cases exist. Here we will define the system used by our dispatch class
to determine the appropriate function to call. For the purpose of this
explanation, we will refer to class hierarchies as being to the "left"
or "right" of each other. This is simply the order of templating. In
the above examples, the c1 hierarchy is to the left of that of c2. First
we will explain the two-dimensional case, then we will generalize.
The easiest way to think of the 2D detection algorithm is to imagine a
breadth-first search up the left hierarchy, starting with the leaves, in
the order in which they were inserted. When a node is visited in this
search, a complete breadth first search is done of the right
graph, taking each node from this search and checking if a specific
function matches for the two classes. The first time such a function is
found, the search terminates.
This description neglects to explain the order in which multiple
parents will be expanded. Fortunately, that is well defined: parents
will be searched in the order that the edges were added. Thus the first
connected parent will take precedence over the second and so on. This
can lead to some peculiarities which we will describe below. When the
system that infers relationships is developed, the system will add
vertices as it discovers them, and will give parental precedence to
vertices in this order also. We like to refer to the ancestor with
priority as an honored ancestor, simply because it agrees with our
sense of humor.
The N dimensional detection system is best described recursively:
The right case from above provides the termination of the recursion
(when only one class remains, do a breadth-first search, checking each
node with the, now complete, list of types for an appropriate function).
Otherwise, do a breadth-first search on the left-most tree, at each
node recursing on the trees to the right of the current one.
The other obvious resolution system is a "depth minimization" one. Such
a system would choose the function that requires the smallest number of
steps up the hierarchy for all of the classes. While such a system
would not be difficult to implement, we felt that it would yields
results that can be more difficult to predict, and requires yet another
ambiguity resolver when two different functions provide the same depth
value. Thus we chose this method, which has clearly defined and easily
documented preferences.
Peculiarities in Resolution
As mentioned, this does lead to some peculiarities in
resolution; however, all of them conform to the definition given above.
Consider the object hierarchies represented below, darker lines
represent honored ancestors.
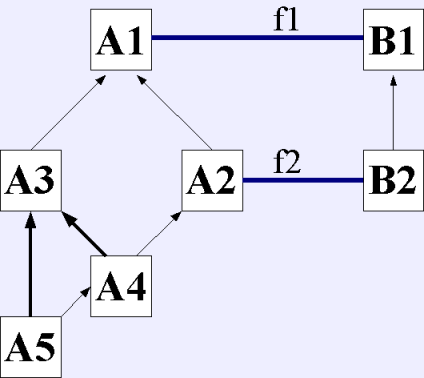
Now consider what happens when the dispatch is called with objects of
type A5 and B2. During the search A5 will expand node A3 before A4.
Thus A3 will expand A1 before A2 gets expanded by A4. When A1 is
checked, it will match with f1. Unfortunately, f2 is arguably the
correct function to call in this case. If the user wished to achieve
that result, she could report the class hierarchy used below. This
hierarchy is slightly different then the true one, but is not
meaningfully different in cases other than those of the type described
here.
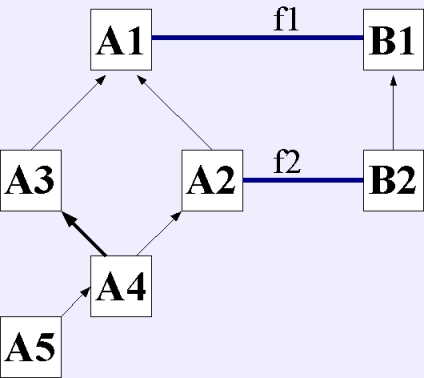
Interestingly, this example also points out a quirk with automatic
hierarchy inference. Consider a situation whose "true" hierarchy is
represented by the first image. When A5 is added to the inheritance
hierarchy, the inference system can determine that A5 is a child of A4;
however, since it cannot distinguish between children and
grandchildren, it cannot determine that A5 is a child of A3, since it
might be able to accomplish the dynamic cast by way of A4. Thus, these
triangular relationships cannot be determined. Some people might
consider this a feature, as it will correctly deal with the example
given here, but whatever one wishes to call this fact, it needs to be
noted.
Automatic Inference
The inference engine works by determining the tree
based on the functions that are provided to it. When a function is
added (through the same method as above), each type is placed into the
tree and then the function is added between their codes (just as a user
would do). When an element is placed into the tree, we use the name of
the class (provided by RTTI) to determine if it is already in the tree.
If so we return the appropriate id. If it is not in the tree, we use
dynamic casts, starting from the leaves, to determine the items
position in the tree. It is at this part of the process that we
construct an object of the appropriate type, which is why it must be
default constructible. If our system of dispatch were put into the
compiler, we would not need this restriction as the compiler can use
the extra information that it already possess to determine these
relationships.
Once we have determined what a class's parents are, we check each of
the parent's children to decide if they are really children of our new
class. If they are, we insert the new class between the parent and
child, otherwise we simply attach the new class as a child of the
parent.
An inferential dispatcher can be constructed far more easily than an
normal one, since it does most of the work for you. Thus the following
code is enough to generate a fully functional inferential dispatcher:
int f(A1*, B1*);
int f(A1*, B2*);
int f(A2*, B2*);
int f(A4*, B1*);
int f(A4*, B2*);
int main()
{
infer_disp<A,A,int> d(f);
d.template add<A2,A>(f);
d.template add<A1,A1>(f);
d.template add<A3,A4>(f);
}
Memoization
Currently our system uses a hash table to accomplish
memoization. When a dispatch is requested, the hashtable is checked to
determine if the appropriate function is already known. If it is not,
we check through the tree in the manner described above. The result
from this check is placed into the hashtable and then returned.
Our current implementation uses RTTI to determine the name of each
class and hashes on the concatenation of the two names. We are planning
on switching to a more efficient hashing scheme later, but currently we
are just focusing on proof of concept. Once we are satisfied with the
stability of it, we will begin optimizing our dispatch and will post
benchmarks against other systems we find.
Code and Links
Anyone may use our code at their own risk.
| makefile | Main Dispatch Class | Auto-inferential Dispatcher | Internal Graph | test program | Tar filed everything |
We will add links to this section as we find them:
- General over view and description of multiple dispatch, and implementation in Perl
- A method for implementing multiple dispatch in C++
Last modified 2003-10-07 22:15 EST