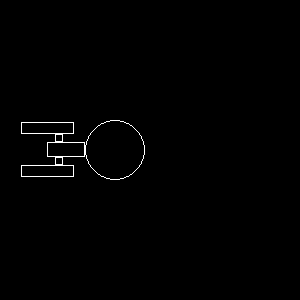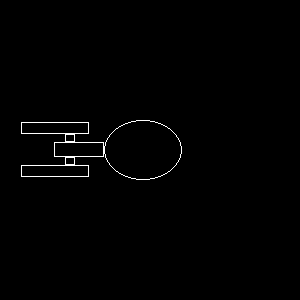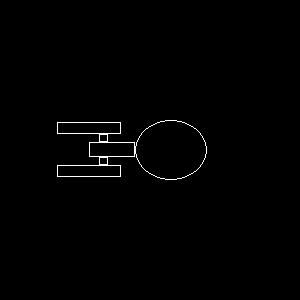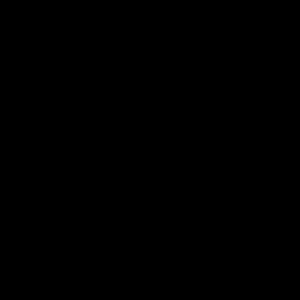2D Transformations and the 2D Viewing Pipeline
Part 1: 2D Tranformations
The ability to perform transformations on objects in an image is
an important feature of a graphics system. Operators were added to this
system which allow the user to create 2D transformation matrices that
perform the following transformations:
- scale around (0, 0)
- scale around an arbitrary point, with the x-scale direction
oriented to a specified angle
- translate
- rotate around (0, 0)
- rotate around an arbitrary point
In addition, helper functions were created that perform matrix
multiplication, reset a matrix to the identity, reset a matrix to the
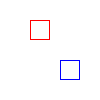
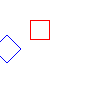
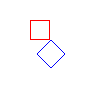
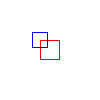
zero matrix, and print a matrix. Below are some sample images created
using these methods. The original polygons are in red, and the tranformed
ones are in blue. The images are of translation, rotation of PI/4 about
(0, 0), rotation of PI/4 about (80, 40), scaling by .8 in x and y,
and respectively.
Part 2: The Starship Enterprise
The next task was to create an image of the Starship Enterprise
by applying the transformation tools developed in the previous task
to a unit circle and square. Below is the generated image.
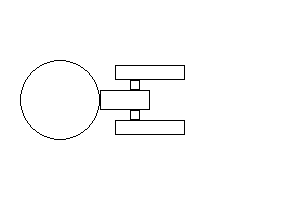
Part 3: Animating the Starship Enterprise
The next step was to create an animation of the Enterprise orbiting
a planet.

Part 4: The Viewing Pipeline
The final task consisted of creating a 2D viewing pipeline that would
allow the designer to pan around the image. The animation below is an
example of this feature. The viewing pipeline moves in a diamond shape
that shadows the motion of the Enterprise.

Extensions
As an extension, we used the transformation matrices that we had created
to make an animated gif of the Enterprise going to warp speed. The
parts of the Enterprise are stretched and then shrunk over time, and
a filled polygon was added at the end to create the effect of an
explosion.
Questions
-
Who did you work with on this assignment, and what tasks did each
of you do?
I worked with Casey Smith, and we shared the work on most of the
tasks.
-
Describe the mechanism you developed for handling the global
transformation parameters and matrix.
The "global transformation parameters" weren't really global, they were
local to the test program. Each new graphics object had its own
transformation matrix, and each of these was passed to the appropriate
drawing function (polyLineM, drawUnfilledCircleM, drawFilledCircleM).
The transformation was applied to the points in the the draw functions.
-
Describe the mechanism you developed for handling the viewing
pipeline parameters and transformation matrix.
For this assignment, the global transformation parameters were
hardcoded into the test programs, and the matrix was constructed by
translating and scaling the View Transformation Matrix using the
translation and rotation functions. In the future, however, a function
will be created that will take in the points at the lower left and
upper right of the viewing window and the desired scale and will
perform the translation and rotation on the VTM.
-
Once you had the code in place, what was the process and how
difficult was it to modify the view window and the position of the
Enterprise?
The transformation functions made it very easy to move the objects in
the scene and to change the view window. To change the position of the
enterprise, simply apply the same translation or rotation to each piece
of the figure. This will, of course, become even simpler when we have
created a hierarchical modeling system in which individual graphical
elements can be combined into one object and tranformed as a unit.
Moving the viewing window is equally easy. Points are stored for the
lower left and upper right corners of the view window, along with the
desired dimensions of the output image. Changing the viewing window is
as simple as changing the points for the corners of the viewing window
and then applying the transformation matrix to the image objects (lines,
circles, etc.).
-
If you extended this assignment in any way, describe what you did
and how you did it. Include pictures, or links to pictures that
show what you did.
As an extension, we created an image of the Starship Enterprise going
into warp speed (see above). We just created series of images in which
the Enterprise was stretched, followed by a series of images in which it
was collapsed into an explosion (a filled polygon).