Lab 3. Scanline Fill Algorithms

M. Stone and A. Pshenichkin. 9.26.04.

Scanline Fill for Polygons

We used the scanfill skeleton as a basis for our code, although we rewrote it to use STL vectors and multimaps. This function takes a list of points and a color value and creates a polygon constructed by connecting the points in sequence, filled completely with the given color. The algorithm works for all polygons as long as the lines that define it do not cross.

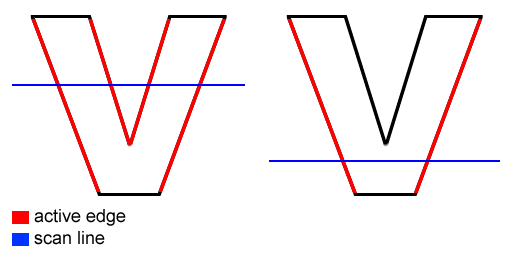
A scanline fill scans through the lines of a polygon individually, creating a list of where line segments start and end. As it iterates through an image row-by-row, it keeps an Active Edge List, which stores information on which of a polygon's component line segments contribute to the appearance of a given line. For example, in a V-shaped polygon, one would see all four non-horizontal lines in the AEL as it started scanning near the top of the image, but only the two that meet at the lower vertex would be on the AEL if we were on a row that was already past the junction of the upper/inner two lines, as is illustrated more clearly in this figure:

Our AEL is a vector, which allows it to automatically resize itself when necessary (by doubling itself and copying all elements) and generate its own iterator. Since the iterator is random-access, we can jump around in the list and navigate it bidirectionallly.

Scanline Fill for Ellipses

On its face, filling ellipses in standard orientation (and circles) is a very simple problem. By introducing the arbitrary rotation requirements, however, we do somewhat complicate things.

Since ellipses can be treated as linear transformations of a unit circle, one can find the intersection of a line with an ellipse by calculating that linear transformation and applying its inverse to the line. Calculating the intersection of a unit circle and a line is relatively trivial, and we can reverse the transformation to convert those points of intersection back into the original coordinate system. So we can simply scan through the ellipse by applying our transformation to each scan line.

To actually calculate points of intersection, we use a quadratic equation with the following values of a, b, and c:

a = (x2-x1)^2 + (y2-y1)^2
b = -2(x1^2) + 2(x1)(x2) - 2(y1)(y1-y2)
c = (x1)^2 + (y1)^2 - 1

Parser

To facilitate the drawing of complex images, we created a parser. Data input from a properly-formatted text file can be read directly into the drawing program. Filled polygons are created by specifying a color (the list of colors is defined at the beginning of the file) and a list of verteces. In our current implementation, the total number of points in the list must be given for it to be processed correctly. Polylines (which can also be used to draw unfilled polygons) also take a color and a vertex list. Circles can be specificed by a center and a radial point, while ellipses can be described using the center and a radial point on each of the two axes. For example, the input used to draw the Starbridge looks like this:

Colors {
blue-white 210 210 255 255
silver 234 234 246 255
black 0 0 0 255
dark-grey 71 71 76 255
light-grey 103 110 108 255
navy 22 30 81 255
teal 0 153 102  255
very-dark-grey 45 45 47 255
white 255 255 255 255
}


Circle {
center 414 661
radial-point 382 696
color blue-white
}

Circle {
center 373 557
radial-point 322 504
color blue-white
}

Polygon {
color silver
vertex-list 10 {
446 634
433 657
434 673
462 710
492 729
511 731
542 721
555 710
529 658
446 634
}
}

Note that the polygons in this image all specify one of their points twice. This is because some of the plates on the Starbridge have outlines in a different color, which are drawn by linking those same verteces with a Polyline. Therefore, we added that extra point to the definitions of all our polygons so that it would be easier to specify the border lines later.

Anti-Aliasing and PolyLine

We can anti-alias the edges of our objects by simply calling DrawEllipse and DrawLine on the edge contours from inside the algorithm. At the moment, our renderer is set to do this automatically.

The implementation of PolyLines (sets of connected lines that don't close like a polygon) requires only a trivial modification of our DrawPolygon.

Resultant Images

M. Stone and A. Pshenichkin.